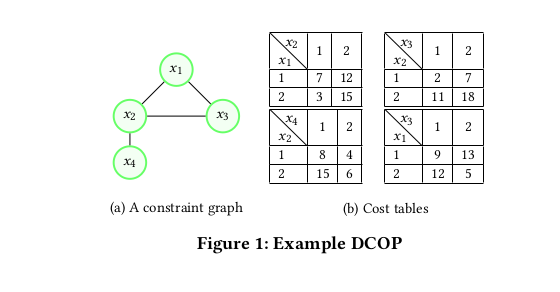
Applying Population-Based Algorithms to Solve Large (F)DCOPsDistributed Constraint Optimization Problems (DCOPs) are a widely studied constraint handling framework. The objective of a DCOP algorithm is to optimize a global objective function that can be described as the aggregation of a number of distributed constraint cost functions. In this work, we present two new population-based algorithms, namely Anytime Evolutionary DCOP (AED) and Particle Swarm Based F-DCOP (PFD), that adapt evolutionary optimization and Particle Swarm Optimization respectively to solve (F)DCOPs. In our theoretical analysis, we prove that both AED and PFD are anytime. Finally, we present empirical results indicating both of our algorithms outperform the state-of-the-art (F)DCOP algorithms in terms of solution quality and computation overhead. AAAI 2020 AAMAS 2020 |
|
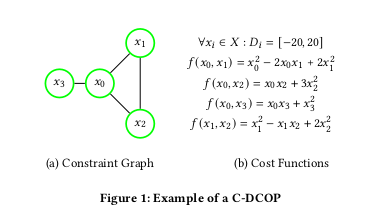
Applying Local Search Based Algorithms for solving Continuous DCOPsDistributed Constraint Optimization Problems (DCOPs) are a suitable formulation for coordinating interactions (i.e. constraints) in cooperative multi-agent systems. The traditional DCOP model assumes that variables owned by the agents can take only discrete values and constraints’ cost functions are defined for every possible value assignment of a set of variables. While this formulation is often reasonable, there are many applications where the decision variables are continuous valued and constraints are in functional form. To overcome this limitation, Continuous DCOPs (C-DCOPs), an extension of the DCOPs model has been proposed that is able to formulate problems having continuous variables. The existing methods for solving C-DCOPs come with a huge computation and communication overhead. In this paper, we apply continuous non-linear optimization methods on Cooperative Constraint Approximation (CoCoA) algorithm, which is a non-iterative, fast incomplete local search approach for solving DCOPs. We empirically show that our algorithm is able to provide high-quality solutions at the expense of smaller communication cost and execution time compared to the state-of-the-art C-DCOP algorithms. AAMAS 2021 |
|
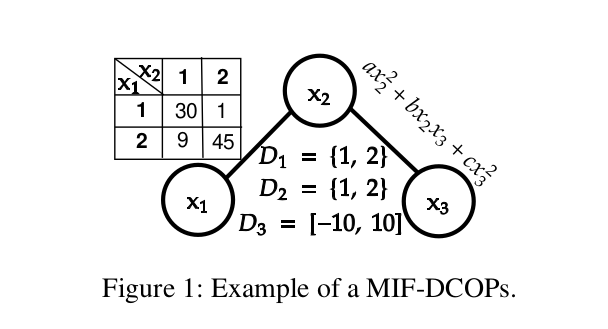
Learning Optimal Temperature Region for Solving Mixed Integer Functional DCOPsDistributed Constraint Optimization Problems (DCOPs) are an important framework that models coordinated decision-making problem in multi-agent systems with a set of discrete variables. Later work has extended this to model problems with a set of continuous variables (F-DCOPs). In this paper, we combine both of these models into the Mixed Integer Functional DCOP (MIF-DCOP) model that can deal with problems regardless of its variables’ type. We then propose a novel algorithm, called Distributed Parallel Simulated Annealing (DPSA), where agents cooperatively learn the optimal parameter configuration for the algorithm while also solving the given problem using the learned knowledge. Finally, we empirically benchmark our approach in DCOP, F-DCOP and MIF-DCOP settings and show that DPSA produces solutions of significantly better quality than the state-of-the-art non-exact algorithms in their corresponding setting. IJCAI 2020 |
|